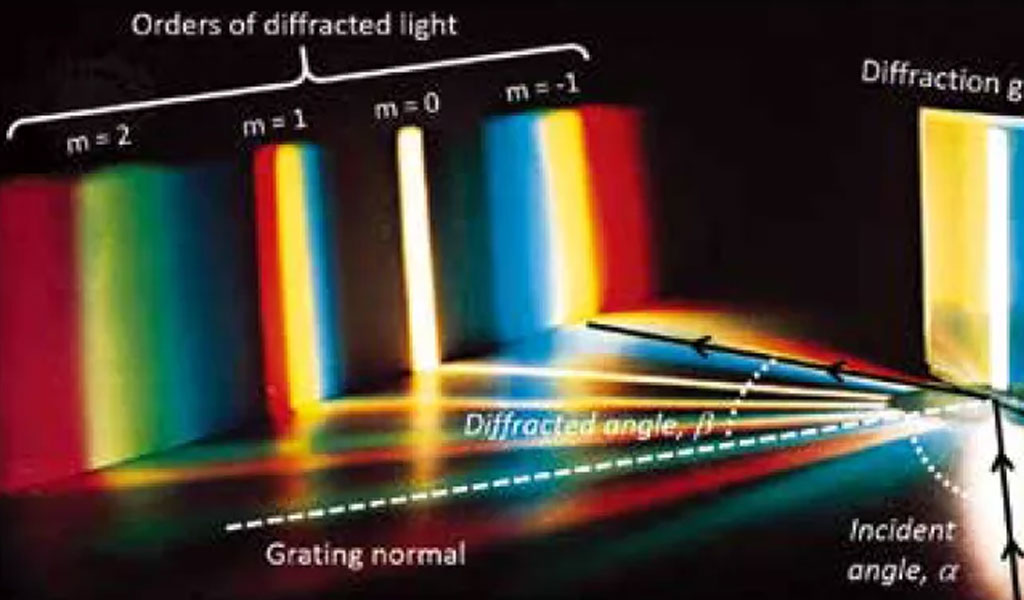
Diffraction gratings are optical components that disperse light into its constituent wavelengths, making them indispensable in various scientific and engineering applications, including spectroscopy, telecommunications, and optical sensing. Etched diffraction gratings, in particular, are fabricated by creating periodic structures on a substrate using techniques such as lithography and etching. The simulation of these gratings using scalar diffraction theory provides a powerful tool for understanding and optimizing their performance.
Scalar diffraction theory is a simplified approach to modeling the behavior of light as it interacts with diffractive structures. It assumes that the light waves can be described by a scalar field, neglecting the vector nature of electromagnetic waves. This approximation is valid when the feature sizes of the grating are much larger than the wavelength of the incident light. The theory is particularly useful for simulating the far-field diffraction patterns of gratings, which are of primary interest in many applications.
Historical Context
The study of diffraction gratings dates back to the early 19th century, with significant contributions from scientists such as Joseph von Fraunhofer and Henry Augustus Rowland. Fraunhofer’s work on the spectral analysis of light using gratings laid the foundation for modern spectroscopy.
Rowland’s concave gratings, which combined the functions of a grating and a mirror, further advanced the field by improving spectral resolution and efficiency.
The development of scalar diffraction theory can be traced back to the work of Augustin-Jean Fresnel and Gustav Kirchhoff. Fresnel’s wave theory of light provided a framework for understanding diffraction, while Kirchhoff’s diffraction formula offered a mathematical description of the phenomenon. These early theories paved the way for more sophisticated models, including the scalar diffraction theory used today.
Principles of Scalar Diffraction Theory
Scalar diffraction theory is based on the Huygens-Fresnel principle, which states that every point on a wavefront can be considered a source of secondary wavelets. The interference of these wavelets determines the diffraction pattern. The theory assumes that the amplitude of the light wave can be described by a scalar function, ignoring polarization effects.
The fundamental equation of scalar diffraction theory is the Fresnel-Kirchhoff diffraction formula, which relates the complex amplitude of the light wave at a point in the diffraction pattern to the amplitude distribution on the grating. For a grating with a periodic structure, the diffraction pattern can be expressed as a Fourier series, where each term corresponds to a diffraction order.
Simulation of Etched Diffraction Gratings
The simulation of etched diffraction gratings using scalar diffraction theory involves several steps:
- Definition of the Grating Structure: The first step is to define the geometric parameters of the grating, including the period, depth, and shape of the etched features. These parameters determine the diffraction properties of the grating.
- Incident Light Wave: The incident light wave is specified in terms of its wavelength, amplitude, and phase distribution. The wave is assumed to be monochromatic and coherent.
- Calculation of the Diffraction Pattern: Using the Fresnel-Kirchhoff diffraction formula, the complex amplitude of the light wave at points in the far-field diffraction pattern is calculated. This involves integrating the contribution of each point on the grating surface to the diffraction pattern.
- Analysis of the Diffraction Pattern: The diffraction pattern is analyzed to determine the intensities of the various diffraction orders. This information is used to evaluate the performance of the grating, including its spectral resolution and efficiency.
Mathematical Formulation
The mathematical formulation of scalar diffraction theory for etched diffraction gratings involves the following key equations:
Fresnel-Kirchhoff Diffraction Formula:
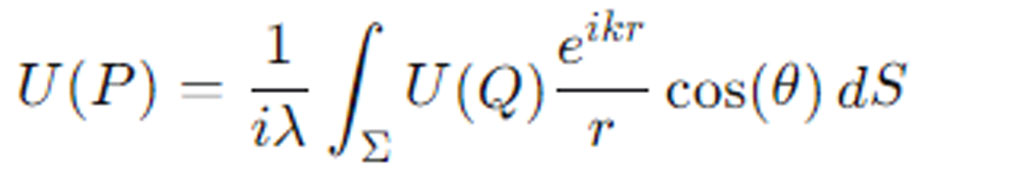
where U(P) is the complex amplitude at point P in the diffraction pattern, U(Q) is the complex amplitude at point Q on the grating surface, λ is the wavelength of the incident light, k is the wave number, r is the distance between points P and Q, and θ is the angle between the normal to the grating surface and the direction from Q to P.
Fourier Series Representation:
where U(x,y) is the complex amplitude of the light wave at point (x,y) on the grating surface, ,An are the Fourier coefficients, and d is the period of the grating.
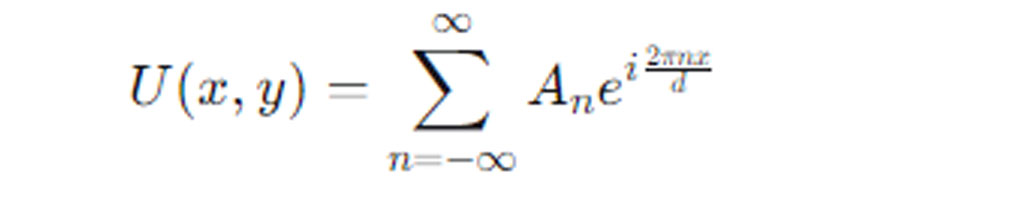
Diffraction Efficiency:
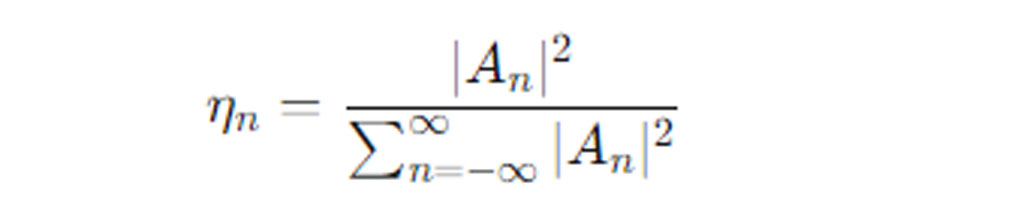
ηn is the diffraction efficiency of the n-th order.
Numerical Implementation
The numerical implementation of scalar diffraction theory for simulating etched diffraction gratings involves discretizing the grating surface and solving the diffraction integral numerically. This can be achieved using various numerical methods, including the Fast Fourier Transform (FFT) and the Finite-Difference Time-Domain (FDTD) method.
- Discretization: The grating surface is divided into a grid of points, and the complex amplitude at each point is calculated based on the incident light wave and the grating structure.
- FFT Method: The FFT method is used to compute the Fourier coefficients of the complex amplitude distribution on the grating surface. This provides a efficient way to calculate the diffraction pattern in the far field.
- FDTD Method: The FDTD method is used to simulate the time-domain evolution of the light wave as it interacts with the grating. This method is particularly useful for simulating the near-field behavior of the grating.
Comparison of Simulation Methods
The following table compares the FFT and FDTD methods for simulating etched diffraction gratings:
| Feature | FFT Method | FDTD Method |
|---|---|---|
| Computational Efficiency | High | Moderate |
| Accuracy | Moderate | High |
| Suitability for Far-Field | Excellent | Good |
| Suitability for Near-Field | Poor | Excellent |
| Handling of Complex Structures | Moderate | Excellent |
| Memory Requirements | Low | High |
| Time Requirements | Low | High |
Applications of Scalar Diffraction Theory
Scalar diffraction theory has a wide range of applications in the simulation and design of etched diffraction gratings. Some of the key applications include:
- Spectroscopy: Diffraction gratings are used in spectroscopy to disperse light into its constituent wavelengths, allowing for the analysis of spectral lines. Scalar diffraction theory is used to simulate the diffraction patterns of gratings, optimizing their design for high spectral resolution and efficiency.
- Telecommunications: In optical telecommunications, diffraction gratings are used for wavelength division multiplexing (WDM), where multiple wavelengths are transmitted over a single optical fiber. Scalar diffraction theory is used to simulate the performance of gratings in WDM systems, ensuring efficient and reliable data transmission.
- Optical Sensing: Diffraction gratings are used in optical sensing applications, such as biosensors and chemical sensors, to detect changes in the refractive index of a sample. Scalar diffraction theory is used to simulate the response of gratings to changes in the refractive index, optimizing their sensitivity and selectivity.
- Laser Systems: In laser systems, diffraction gratings are used for wavelength selection and stabilization. Scalar diffraction theory is used to simulate the diffraction patterns of gratings, ensuring stable and efficient laser operation.
Case Studies
Case Study 1: Simulation of a Blazed Grating
A blazed grating is a type of diffraction grating designed to concentrate the diffracted light into a specific order, typically the first order. The blaze angle of the grating is optimized to maximize the diffraction efficiency in the desired order.
Parameters:
- Grating period: 1 µm
- Blaze angle: 17.5°
- Incident wavelength: 632.8 nm
Simulation Results:
- Diffraction efficiency in the first order: 85%
- Diffraction efficiency in the zeroth order: 5%
- Diffraction efficiency in the second order: 2%
The simulation results demonstrate the high efficiency of the blazed grating in concentrating the diffracted light into the first order, making it suitable for applications requiring high spectral resolution.
Case Study 2: Simulation of a Sinusoidal Grating
A sinusoidal grating has a periodic structure with a sinusoidal profile. This type of grating is used in applications requiring a smooth and continuous diffraction pattern.
Parameters:
- Grating period: 2 µm
- Grating depth: 0.5 µm
- Incident wavelength: 532 nm
Simulation Results:
- Diffraction efficiency in the first order: 30%
- Diffraction efficiency in the zeroth order: 20%
- Diffraction efficiency in the second order: 15%
The simulation results show that the sinusoidal grating produces a more distributed diffraction pattern compared to the blazed grating, making it suitable for applications requiring a broad spectral response.
Case Study 3: Simulation of a Binary Grating
A binary grating has a periodic structure with rectangular features. This type of grating is used in applications requiring simple and robust diffraction patterns.
Parameters:
- Grating period: 3 µm
- Grating depth: 1 µm
- Incident wavelength: 405 nm
Simulation Results:
- Diffraction efficiency in the first order: 40%
- Diffraction efficiency in the zeroth order: 10%
- Diffraction efficiency in the second order: 5%
The simulation results indicate that the binary grating provides a balanced diffraction pattern, making it suitable for applications requiring a compromise between spectral resolution and efficiency.
Challenges and Limitations
While scalar diffraction theory provides a powerful tool for simulating etched diffraction gratings, it has several challenges and limitations:
- Vector Nature of Light: Scalar diffraction theory neglects the vector nature of electromagnetic waves, which can lead to inaccuracies in the simulation of gratings with complex structures or polarization-dependent behavior.
- Near-Field Effects: Scalar diffraction theory is primarily suited for far-field simulations and may not accurately capture near-field effects, which are important in some applications.
- Computational Complexity: The numerical implementation of scalar diffraction theory can be computationally intensive, especially for gratings with complex structures or large feature sizes.
- Material Properties: Scalar diffraction theory does not account for the material properties of the grating, such as refractive index and absorption, which can affect the diffraction pattern.
Future Directions
To address the challenges and limitations of scalar diffraction theory, future research should focus on the following areas:
- Vector Diffraction Theory: Developing vector diffraction theories that account for the polarization and vector nature of electromagnetic waves can improve the accuracy of grating simulations.
- Near-Field Simulations: Enhancing near-field simulation capabilities using advanced numerical methods, such as the FDTD method, can provide a more comprehensive understanding of grating behavior.
- Material Properties: Incorporating material properties into diffraction simulations can improve the accuracy of grating performance predictions.
- Computational Efficiency: Developing more efficient numerical algorithms and leveraging high-performance computing resources can reduce the computational complexity of grating simulations.
Conclusion
Scalar diffraction theory provides a valuable framework for simulating etched diffraction gratings, offering insights into their diffraction patterns and performance. By defining the grating structure, specifying the incident light wave, and calculating the diffraction pattern, researchers can optimize grating designs for various applications. While scalar diffraction theory has its limitations, ongoing research and development in vector diffraction theory, near-field simulations, material properties, and computational efficiency promise to enhance the accuracy and applicability of grating simulations.
The case studies presented in this article demonstrate the versatility of scalar diffraction theory in simulating different types of gratings, including blazed, sinusoidal, and binary gratings. Each type of grating offers unique advantages and is suited for specific applications, highlighting the importance of tailored grating designs.
As the field of diffraction gratings continues to evolve, the integration of advanced simulation techniques and experimental validation will be crucial for pushing the boundaries of optical technology. By leveraging the strengths of scalar diffraction theory and addressing its limitations, researchers can develop innovative grating designs that meet the demands of modern scientific and engineering applications.